How the Quest for Counting Prime Numbers, Eratosthenes, and Legendre Sieves Apply to “Instantaneous Zero Trust Microsegmentation with Progressive Improvements”

Recently, my kids challenged me to explain how math applies to real life. This time with a twist: “Not ancient math, but something relevant today!”  

Their curiosity, paired with the recent discovery of the largest known prime (a 41-million-digit behemoth, M136279841 2^136279841-1), inspired me to explore how prime number sieves and sieve theory—both ancient and modern—can help shape today’s cybersecurity solutions. 

This post, like the previous one, is inspired by a question from a customer. Our customer, who manages cybersecurity for a century-old global brewery with hundreds of IT and OT sites, posed a challenging question: 

“We understand that zero-trust microsegmentation can bolster our cyber defenses, but I’m concerned about the lengthy setup process. The learning period alone could take months, and one mistake could disrupt our entire operations. Can you deliver value in weeks or months while ensuring there’s no disruption from a shortened learning cycle?” 

Our Answer: 

“Absolutely! From day one, with no disruption.” 

To explain, let’s look back at ancient methods for identifying and counting prime numbers, which, surprisingly, offer insights into solving modern cybersecurity challenges. The sieve methods pioneered by Eratosthenes and refined by Legendre provide useful frameworks for progressively filtering out risks in zero trust microsegmentation. 

2,500-Year-Old Math: Eratosthenes 

You might have wondered at some point, how many prime numbers are there between 1 and 100? Interestingly, this question has been pondered for at least 2,500 years, if not longer. The most straightforward approach is to check each number from 1 to 100 to see which ones have factors and which are prime. This process looks something like this: 

As you can imagine, this approach requires significant effort, and if we increase the range to 1,000, a million, a billion, or more, it becomes unmanageable.  

Eratosthenes discovered a method to do this much faster, allowing the range from 1 to 100 to be solved in just four layers of the sieve. 

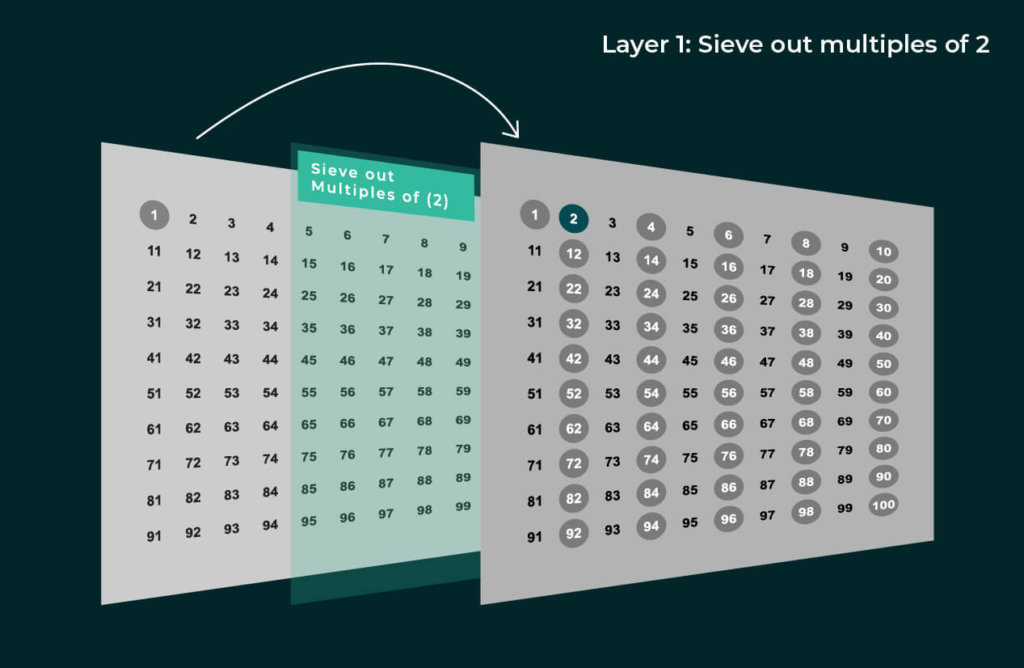
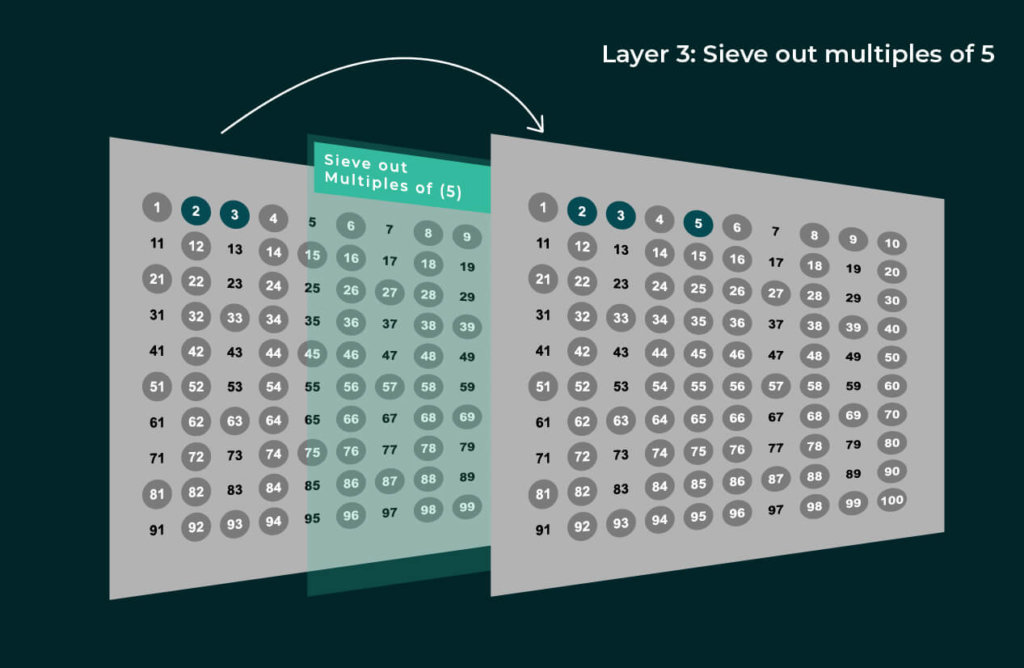
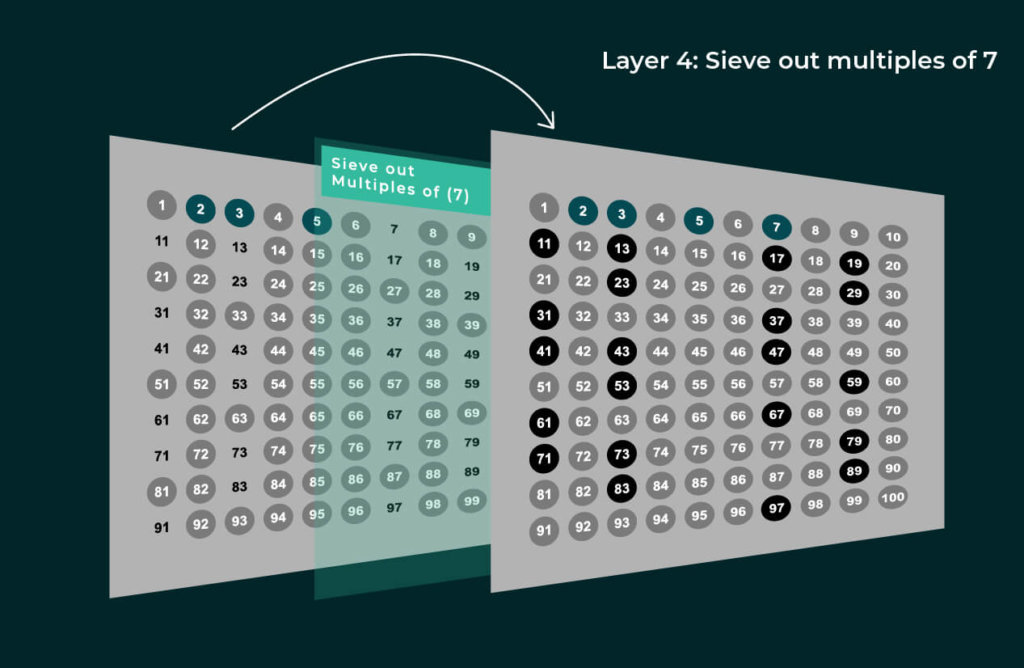
And that’s it! Can you believe that everything remaining is prime? Here’s how it works: 

• All numbers we eliminated are not prime, as they are multiples of 2, 3, 5, or 7. 
• All remaining numbers are not multiples of 2, 3, 5, or 7. 
• The next prime, 11, has no multiples less than 100 that aren’t already multiples of 2, 3, 5, or 7. (If we write out the table of 11, then 22, 33, 55, and 77 are the only multiples, all of which are also multiples of 2, 3, 5, or 7. The next multiple, 121, is greater than 100.) 

The method we’re using is known as the “Eratosthenes Sieve,” developed around 250 BC (so our discovery is about 2,500 years late). More generally, the way it works is that to find primes from 1 to n, we sift through them with a sieve of all primes starting from 2, 3, and so on, up to the largest prime ≤ √n. In each layer, we eliminate multiples of each prime, thereby removing all composites up to n, leaving only the prime numbers. 

18th-Century Math: Legendre 

Fast forward to the 18th century, when Legendre developed a formula to count primes based on the “Eratosthenes Sieve.” 

If we look at the steps we took to sift numbers from 1 to n through the “Eratosthenes Sieve” 

In layer 1, we eliminated multiples of 2 or about 1/2 of the numbers 

Count of Primes < n – (n*(1/2))

In layer 2, we eliminated multiples of 3, or about 1/3 of the numbers. But that double counts multiples of 3 and 2 (or in other words multiples of 6) so we should subtract 1/6 

Count of Primes < n – (n*(1/2)) – (n*(1/3) – n*(1/2*3)) 

In layer 3, we eliminated multiples of 5, or about 1/5 of the numbers. But that double counts multiples of 5 and 2, so we should subtract 1/10, or multiples of 5 and 3, so we should subtract 1/15, but that triple counts multiples of 5, 2, 3, so we should add back 1/30 

Count of Primes < n – (n*(1/2)) – (n*(1/3) – n*(1/2*3)) – (n*(1/5) – n*(1/2*5) – n*(1/3*5) + n*(1/2*3*5))  

In layer 4—no, I’m not going to go through that, as the terms get increasingly complex—but we get the basic idea. 

Here are some observations (these will be very useful when we apply them to zero-trust microsegmentation): 

• Instead of trying to identify and count primes directly, we approach the problem by excluding non-prime numbers. 
• Although each term (sieve layer) makes the result more accurate, each successive term also becomes more complex. 
• If we aim for approximate bounds rather than an exact value, we can achieve reasonable accuracy with only a few terms. 

These are fundamental concepts of sieve theory, as explained by 2022 Fields Medal winner James A. Maynard in his well-known lecture at the Institute for Advanced Study.

 Sieves

• Interested in objects that are output of some inclusion-exclusion process 
• Rather than counting precisely, we want to gain good bounds, but work flexibly

Instantaneous Zero Trust Microsegmentation with Progressive Improvements

In ColorTokens Xshield^TM, we apply these principles by essentially flipping the zero-trust process: 

• Exclusion-Based Filtering
  Instead of attempting to capture or learn every legitimate communication (which can be complex and error-prone), we focus on excluding communications that are invalid or risky. 

• Progressive Layering
  Similar to the sieve method, each layer in zero-trust microsegmentation narrows down communication flows, progressively refining permissions and restrictions. 

• Bounds, Not Perfection
  Just as sieve theory uses bounds for estimating primes, our approach prioritizes establishing a workable security boundary quickly. Rather than striving for perfect segmentation from the start, we achieve finer security through further refinements over time.

This approach addresses the two core concerns our customer highlighted about zero-trust microsegmentation:

• Endless Learning: Uncertainty over whether we have accounted for 100% of legitimate traffic. 
• Fear of Disruption: Shortening the learning cycle might overlook legitimate application communications, causing disruptions.

In our case, we can instantly apply what we learn in sieve layers, and since we always use upper bounds, we ensure there is no disruption.

Let’s walk through an example to illustrate this. Here is the scenario:

An invoicing application in the production environment of the New York Data Center. The sieve will operate as follows:

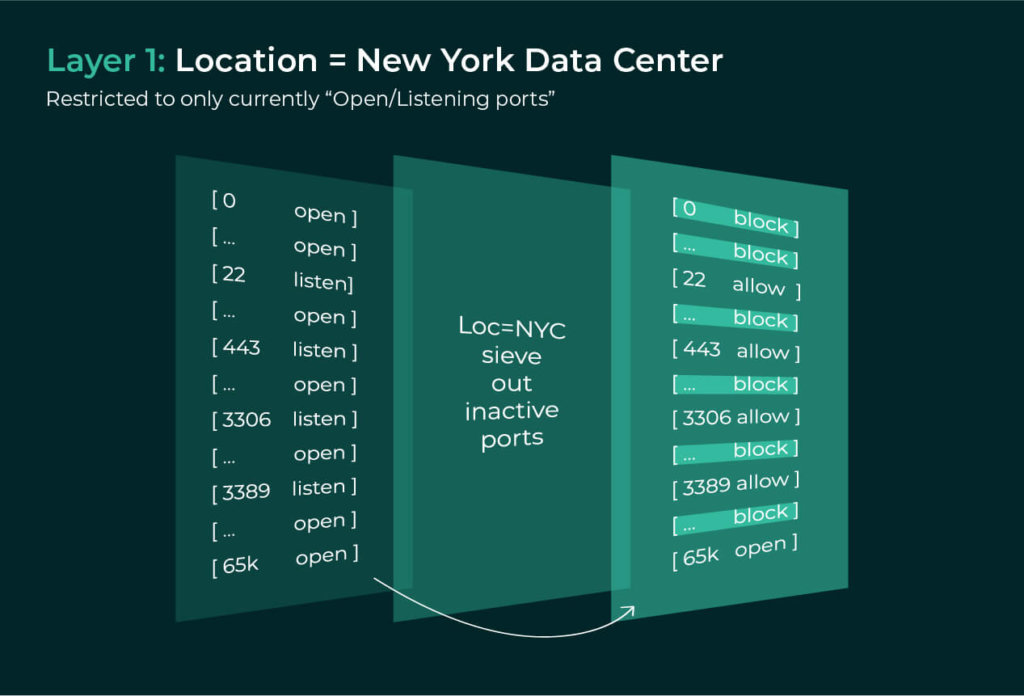
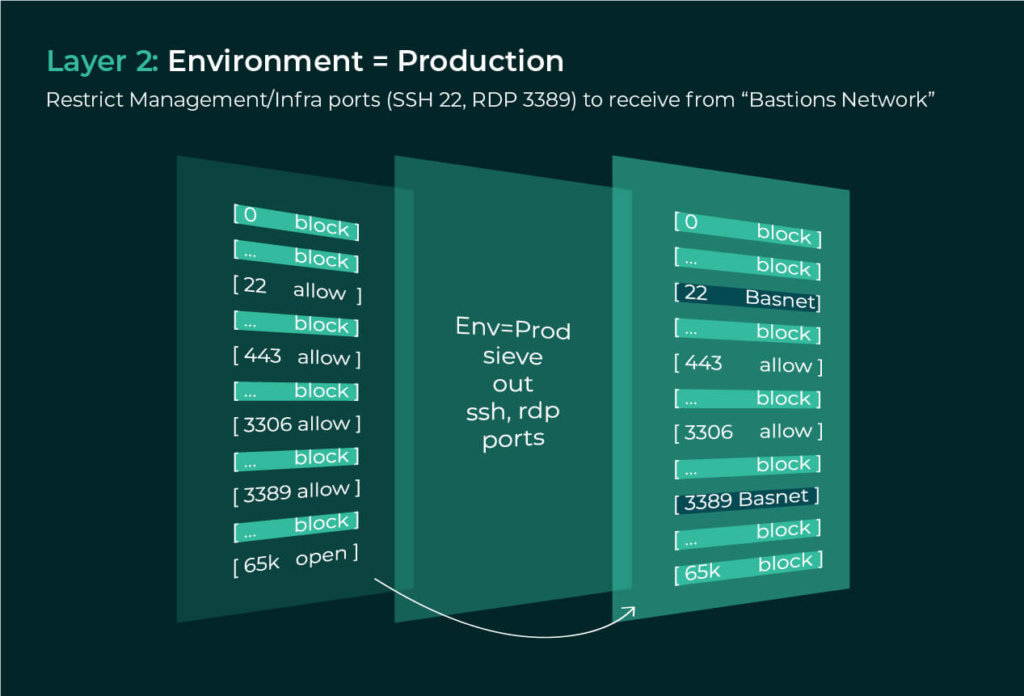
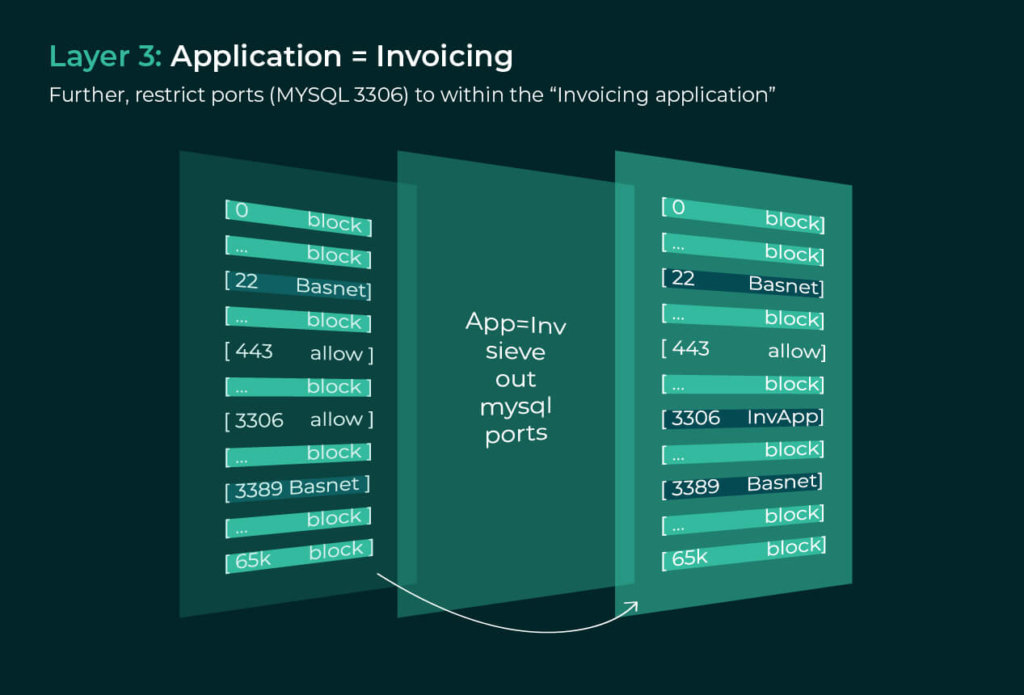
Just within three layers, we can achieve fairly accurate zero trust bounds for legitimate communications. Furthermore, we could enforce the first layer within days across all 1000s of assets in the New York Data Center, the second layer within a week for all 100s of assets across the Production Environment, and the third layer across 10s of assets in the Invoicing Application within a couple of weeks. Finally, since these are all upper bounds, there is no risk of disrupting legitimate traffic.

Bringing Math to Life in Cybersecurity

Just as ancient mathematicians laid the foundation for today’s discoveries in prime numbers, their methods now inspire new ways to solve complex challenges in cybersecurity. By approaching problems from different perspectives and building in layers, we can meet the security needs of critical infrastructure, environments, and applications with minimal disruption—like sieving for primes, but instead ensuring safe communications.

Who would have thought that insights from 2,500-year-old math, along with modern sieve theory, could help tackle the toughest challenges in applying zero-trust microsegmentation in sensitive, high-stakes environments? Yet, that’s precisely what’s happening here. Math is not only an inspiration—it’s a vital tool for solving these real-world challenges.

So, the next time someone asks how ancient and contemporary math apply beyond academia, you can point to Eratosthenes, Legendre, and even Maynard, and the critical role their ideas play in modern cybersecurity.

Do you have questions about accelerating zero-trust microsegmentation with zero disruption? We’re here to help.